Conceptual overview
DUALLy works at two abstraction levels: metamodeling (upper part of the figure below), and modeling (lower part of the figure).
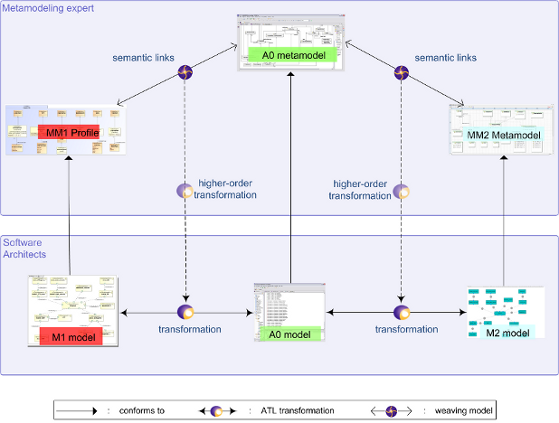
At the meta-modeling level, model driven engineers provide a specification of the architectural language in terms of its meta-model or UML profile. They then define a set of semantic links so as to relate architectural concepts in MM1 with the corresponding elements in MM2. The semantic links are captured by a weaving model. Weaving models are particular kinds of models containing links among models, meta-models or UML profiles.
At the modeling level, software architects specify the SA using their preferred ADL or UML-based notation. DUALLy allows the automatic generation of model-to-model transformations which enable the software architect to automatically translate the M1 specification (written according to MM1) into the corresponding M2 model (conforming to MM2) and viceversa. The generation of the transformations consists in the execution of higher-order transformations that take as input the semantic links between metamodels and produce the model-to-model transformations. The higher order transformations are general, thus the approach of DUALLY is metamodel independent, allowing full interoperability between all the architectural notations whose concepts may be defined through a metamodel or a UML profile.
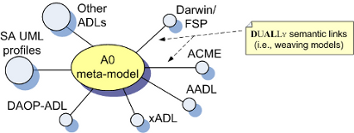
As it can be noticed in the figure, the weaving models (and their corresponding generated transformations) relate MM1 to MM2 (as well as M1 to M2) passing through what we refer to as A0. A0 is a minimal meta-model representing a semantic core set of architectural elements (e.g. components, connectors, behavior); it provides the infrastructure upon which to construct semantic relations among different ADLs. It is specific to software architectural domain and it acts as a bridge among architectural languages. The main benefit of using A0 is the implied star architecture in which A0 is the center of the star while DUALLy's transformation engine is in charge of maintaining the transformation network. The A0 metamodel can be extended if there is the need to relate elements existing in both MM1 and MM2 which are not contemplated in A0.
